


Resources
Videos
The 'Maths Explained' Video Tutorials
One of the biggest problems for learners who are dyscalculic and/or who have trouble in learning mathematics is retaining facts and procedures in long term memory.The best way of addressing these problems is to develop understanding of those maths facts and procedures.
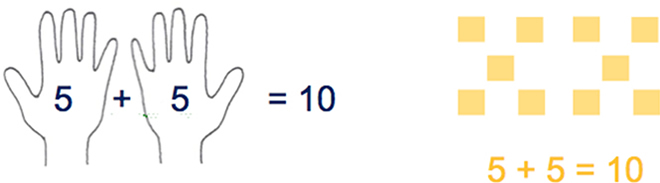
Maths Explained is a collection of video tutorials that teach understanding for basic facts and for many of the key maths topics, such as fractions and division.
Based on 25 years of successfully teaching students who had failed when taught by 'traditional' methods... and based on research from around the world on how children and adults can learn to understand and succeed in maths.
From as little as £2.50 for one tutorial to £60 for over 10 hours of tutorials... and you can play them as many times as you wish.
There are very few thoroughly trained and experienced tutors for maths learning problems in the UK or indeed many other countries. In response to this lack of availability of tutors I have recorded a series of 34 tutorials which address the core topics of maths.
The tutorials can be used for:
- Teacher training (I use the material in my own teacher training sessions)
- Supporting classroom assistants when working with students
- Supporting teachers when working with students
- Independent study by individual students, where the amount of each video watched at one time and the number of times it is watched can be controlled by the student.
(Note that at this stage there is no requirement for a site licence for schools)
Maths Explained is a series of videos which do as the title suggests - the videos explain maths. They are designed primarily for those who struggle to learn maths, but will help anyone who wishes to improve their understanding of basic maths.
Area of a Circle

- The videos explain maths from the beginning, developing an understanding of maths and a confidence in using maths and numbers.
- They are underpinned by Steve's research and experience and also research from experts around the world.
- The videos use simple and clear visual images, often with animations to illustrate the concepts and which are matched to maths vocabulary.
- They are designed to address and circumvent the learning barriers that prevent so many people from succeeding in maths.
- The structure is developmental and inter-linked so that understanding supports memory. This is not about a dependence on rote learning.
- The videos, as a whole or in parts, can be watched repeatedly until understanding is secure. No one will say, 'I've already explained that to you too many times.'
- The videos are not a quick-fix compendium of tricks and mnemonics. They are not games. They build and constantly reflect back on the roots of maths. They are conceptual. They are about understanding maths.
- They are about going back to the earliest concepts and rebuilding a resilient understanding of the basic skills and concepts.
- The videos are not age-specific (for example, there are no dancing clowns or elephants). Any age of learner can benefit from these videos.
"It is such an excellent course and your visuals are great!" Gilly Payne, Professional Course Tutor at the Helen Arkell Dyslexia Centre
"Thank you so much for this program. I wish it were mandatory viewing of every teacher in Australia, for the damage their lack of understanding of learning differences does is too great. My 13 year old has just started your program and for the first time in his life is understanding math!"
The Equation Balance
The tutorials were launched at the end of 2014. They can be purchased individually or as sets via the website There are sample clips from the videos on the Maths Explained website www.mathsexplained.co.uk The tutorials have been purchased in 18 countries, including: South Africa, Australia, Ireland, USA, UK, NZ, Canada, Malta, Spain, Switzerland, India, the Netherlands, Cyprus, Luxembourg, Portugal, Thailand, Singapore and Japan.

Publications - Steve
I have written a range of materials for maths including books, worksheets, a test of thinking style and many papers. My book, 'The Trouble with Maths', won a major special needs (TES/nasen) award in 2004. It is now in 3rd edition. 'More Trouble with Maths' has been translated into Norwegian. 'Mathematics for Dyslexics and Dyscalculics' will be translated into Mandarin in 2017. An appropriately modified edition of 'Mathematics Learning Difficulties, Dyslexia and Dyscalculia' will be published in India in 2017.
|
The International HandbookI compiled and edited the Routledge International Handbook of Dyscalculia and Mathematical Learning Difficulties published in 2015. Contributing authors include: Daniel Ansari, Mark Ashcraft, Robert Ashlock, Lynn Fuchs, David Geary, Russell Gersten, Nancy Jordan, Bob Reeves, Karin Landerl and Robert Siegler. NEWS: A paperback version will be available in October 2017 at £39.99 |
|
|
Mathematics for Dyslexics and Dyscalculics (2017) 4th editionWritten with Richard Ashcroft and published by Wiley Mathematics for Dyslexics, including Dyscalculia will be translated into Mandarin and published in 2018 The 4th edition, a seminal book in this field for more than twenty years, discusses the factors that contribute to the potential difficulties dyslexic learners may have with mathematics, and suggests ways of addressing these difficulties. |
|
|
|
The Trouble With MathsThe award winning book now in 3rd edition: The Trouble with Maths: A Practical Guide to Helping Learners with Numeracy Difficulties. 3rd edition. (2017) Steve Chinn. ISBN 978-1-138-18746-7. |
|
|
|
More Trouble With MathsFrom the Foreword by Professor Maggie Snowling: This is an astonishing book! It should be on the shelves of all professionals in the field of maths education and educational assessment. ISBN 978-1-138-18750-4 'More Trouble with Maths: A complete manual to identifying and diagnosing mathematical difficulties.' 2nd edition (2017) Routledge. There is very little written about diagnosis and assessment of dyscalculia and maths learning difficulties. This book provides a collection of tests and diagnostic procedures, all free to photocopy, which will combine to provide a comprehensive diagnosis for ages 7 to 59 years old. It is a low-cost resource. It is now in 2nd edition. |
|
|
Maths Learning Difficulties and DyscalculiaWritten for the BDA's 40th anniversary series 'Mathematics Learning Difficulties, Dyslexia and Dyscalculia', written for the BDA's 40th Anniversary series, was published in 2012 by the BDA.It is their best-selling title from that series of ten books. 1st edition now sold out. 2nd edition due 2018. This book has also been adjusted in vocabulary for publication in India by Unique Ability Consulting. |
|
|
|
Practical Guides to individual topics in MathsThe 'What to do when you can't' titles are published by Egon Publishers Ltd
These highly accessible books are written for parents, older pupils, students and adults and offer a non-patronising, consistent and developing pathway through basic arithmetic. The 'What to do when you can't" series are available from SEN Books. |
|
|
|
The Fear of MathsWritten for parents and adult dyslexics. The third edition was published in August 2011, re-titled, 'The Fear of Maths and How to Overcome It'. It has been updated significantly. |
|
|
|
Addressing the Unproductive Classroom Behaviours of Students with Special Needs'Addressing the Unproductive Classroom Behaviours of Students with Special Needs', was published by Jessica Kingsley in 2010. This book, a departure from my usual maths books, is based on research done with colleagues in Ireland and the Netherlands. It takes a pragmatic approach to identifying and addressing unproductive classroom behaviours. All the author's royalties go to the Majika school, Hazey View, South Africa. This book was short-listed for a nasen award in 2011. |
|
|
WorksheetsThe eight book set of Worksheets Plus are once again in print. They are available from SEN Marketing |
|
|
Nimcon Big Ideas'Big Ideas' (2017) Steve Chinn, Fiona Goddard and Liz Henning. Numicon/OUP NEW Sept 2017 'Building a secure future in mathematics for every child' Suitable for: Schools with pupils in Upper Key Stage 2 or Key Stage 3 (aged 10 upwards) who need a more secure understanding of key concepts within the primary maths curriculum.
|
|
Publications - Judy Hornigold
|
|
Understanding Maths Learning DifficultiesPublished by OUP |
|
|
|
Help! My Child Has DyslexiaPublished by LDA Originally a guide for parents but now frequently used by TAs, Teachers and Sencos. |
|
|
|
Dyscalculia PocketbookTips, tools and techniques for supporting children whose mathematical ability is affected by dyscalculia. Published by Teachers Pocketbooks |
|
|
|
Dyscalculia Lesson Plans Book 1 and 2 and Resources KitDesigned to help deliver Dyscalculia Lesson Plans in both Book 1 and Book 2 and can also be used independently to support children with mathematical learning difficulties. Published by TTS |
|
|
|
Making Maths Visual and Tactile |
|
SEN books
Books can be ordered direct from the publishers or from
SEN Marketing,
618 Leeds Rd,
Outwood,
Wakefield, WF1 2LT
Tel: 01924 871 697
Useful Sites / Resources
Primary
- www.mathsexplained.co.uk (Tutorials that address the core topics in maths in a dyslexia/dyscalculia friendly way)
- www.stevechinn.co.uk
- www.wordshark.co.uk/numbershark.aspx
- www.dynamomaths.co.uk
- The 'What to do when you can't …¦.' series of maths books by Steve Chinn
- Chinn, S. 'Maths learning difficulties, dyslexia and dyscalculia.' British Dyslexia Association
- Emerson, J and Babtie, P (2014) The Dyscalculia Solution, Bloomsbury
- Hornigold, J. 2017, 'Understanding Maths Learning Difficulties', Open University Press
- Hornigold, J, 2013 'Dyscalculia Lesson Plans' Nottingham. Special Direct
- Chinn et al (2017) 'Numicon: Big Ideas.' Oxford University Press. Suitable for: Schools with pupils in Upper Key Stage 2 or Key Stage 3 (aged 10 upwards) who need a more secure understanding of key concepts within the primary maths curriculum.
- Dyscalculia Screener - Dynamo Assessment (6-9yrs) www.dynamomaths.co.uk
- Council for the Registration of Schools Teaching Dyslexic Pupils (CReSTeD): http://www.crested.org.uk
- R. Ashlock (2010) 'Error Patterns in Computation' 10th edn Pearson
- Chinn, S. (2017) 'The Trouble with Maths' 3rd edn. Routledge
- Chinn, S. and Ashcroft, R. (2017) 'Maths and Dyslexia and Dyscalculia: A Teaching Handbook' 4th edn. Wiley
- Henderson, A. (2012) 'Dyslexia, Dyscalculia and Mathematics: A Practical Guide' 2nd edn. Taylor and Francis
- www.mathsexplained.co.uk (tutorials that address topics in a visual and non-age specific way)
Secondary
- dyscalculia-screener.co.uk/ , which claims to be, 'the World's only post 16 screener'.
- Mathematics Pro a GCSE revision app.
- Moorcraft, P. (2015) 'It Just Doesn't Add Up: Explaining Dyscalculia and Overcoming Number Problems for Children and Adults' Original Paperback
- www.mathsexplained.co.uk (tutorials that address topics in a non-age specific way)
- stemreader.org.uk is a Windows application with tools to help read and explore equations. With STEMReader you can hear equations read aloud and see the transcript on screen, break down equations into simple chunks to make them easier to understand and check the meaning of unfamiliar symbols.
Further Education
- Moorcraft, P. (2015) 'It Just Doesn't Add Up: Explaining Dyscalculia and Overcoming Number Problems for Children and Adults'. Original Paperback
- www.mathsexplained.co.uk (tutorials that address topics in a non-age specific way)
- dyscalculia-screener.co.uk A screener for post-16
- Swipes app An intuitive to-do list which gives the fastest way to organise any list of tasks into priorities, scheduled events and history of accomplishments
- www.todoist.com. Another App for organising.
- www.mathscentre.ac.uk Resources for learners in HE and those applying for HE
- stemreader.org.uk is a Windows application with tools to help read and explore equations. With STEMReader you can hear equations read aloud and see the transcript on screen, break down equations into simple chunks to make them easier to understand and check the meaning of unfamiliar symbols. untimeapp.com A timer app that shows how much time is left in a visual way
(With gratitude to Pete Jarrett of Tutorum.co.uk for his assistance in suggesting resources for FE and HE sections. Note: Pete does assessments for dyscalculia.)
Articles / Blog - Steve Chinn
Maths Learning Difficulties and Dyscalculia in Adults and Older Learners
I have long wanted to write something about dyscalculia and maths learning difficulties in adults. It is a tricky topic. I was on a sunny holiday. I'd read my book and was left with lying in the sun (I'm part lizard) and thinking that I pretty much know which bits of maths I want to try and explain. What I don’t know is how to convince potential readers to become actual real readers.
So, here is the broad structure of my Blog. There are no rules about where to start or what order to follow. My only plea is that you bear with me and somehow read as much as possible. The bits support each other and, hopefully, you. Try to be an active reader. Make notes and comments as you progress through each section. Talk ideas through with yourself or someone who is happy to listen and comment.
What are possible causes of difficulties with maths?
What maths do adults need (or might find useful)?
How do these difficulties impact on life?
What learning might help? (Nothing works for everyone, but what I suggest has been used by me in my four decades of teaching and much is under-pinned by research. But still not a guarantee.).
I started to work with dyslexic students in 1981. At that time (early days in dyslexia history) books that were written at a reading level my students could decode were too young in content and appearance. I am going to try to avoid that with this maths Blog. Rephrasing, I am going to try and present some of the key, basic level maths in an adult-friendly way. So, I have no cartoons or busy, bright pictures. I will use visual images, but, hopefully, ones you will find help you to understand the concepts and ideas that make maths understandable and useful.
Enough!
Let’s look at some research into what maths adults need in life. This work comes from Australia (Maria Northcote and Alistair McIntosh). I have trained teachers in more than thirty countries. Maths difficulties are international.
They found:
The extent to which mental maths dominated was striking. 84.6% of all calculations involved some metal maths, compared to 11% for written maths and 6.8% for use of calculators.
Almost 60% of all calculations required only an estimate. 24.9% of all calculations involved in this research involved time.
Addition (45.7%) and subtraction (42.5%) were the most common operations used.
It appeared that over two thirds of calculations reported were at a level within the range of an average 8 – 9 year old child. In other words, that's where they came in the curriculum.
So, when the British Prime Minister suggests that students should have to (mandatory) study maths to the age of eighteen, he is, hopefully, not talking about calculus. He's going to have to find a way (and a programme) that teaches basic maths in a style that is acceptable to young adults. That's going to need some research and pragmatic work. (I try to get the word, 'pragmatic', at least once into anything I write).
You might have guessed that I'm going to attempt to do that in this blog, so bear with me, please.
Next I want to consider is what are possible causes of difficulties with maths? It can be helpful to understand yourself as a learner. A sort of self-awareness, an understanding of why you have not 'got on' with maths so far.
Sad to say, a big contributor is the curriculum, how it is taught and the influence of long held beliefs, such as 'everyone can (rote) learn the times tables.' A good friend gave me a maths text book from the early nineteenth century for my recent (big number) birthday. So, over 200 years ago. I quote what it says about times tables facts and the times tables square:
By this table the product of any two figures will be found in that square which is on a line with the one and directly under the other. Thus, 56. The product of 7 and 8, will be found on a line with 7 and under 8: so 2 times 2 is 4: 3 times 3 is 9 etc - In this way the table must be learned and remembered. If only it were that simple and guaranteed!
What I found after many years of teaching mathematics to dyslexic students is that the facts they were most likely to retain in long term memory were those for 1,2, 5 and 10. Sometimes it pays to work with what you have and with the facts around 1,2,5 and 10 you can work out all the others and learn some maths concepts as a bonus. More of this later.
What maths do adults need (or might find useful)?
Well, in many situations such as keeping a budget for general spending, setting a budget for a holiday, tipping in a restaurant, buying the right amount of paint for decorating a room, shopping in general, driving, working out the times for a journey, any do-it-yourself project, cooking, gambling, gardening. In other words, there are lots of situations. However, few are directly related to the maths taught in schools. We use estimation in a lot of these situations. More on that later, too. (Sounds like a strategy I'm using to keep you reading this Blog).
How do these difficulties impact on life?
In most of the examples above, the negative impact is likely to result in over-spending, poor financial planning, and/or feeling embarrassed.
What learning might help?
For me, the bottom line is that we address the basics. We start at the beginning. Maths is a subject that builds, that is, it is very developmental. Without the basics being securely understood and accessible, progress is unlikely and unreliable. And, by this, I don’t mean just learning the times tables facts. It's more complicated, and yet more simple, than that. Bear with me I'm heading there.
Without the basic it will be difficult to explore more advanced avenues and topics And, as ever, it's not what you learn. It's how you learn it. (I think it is unlikely that an over-reliance on rote learning will lead to deep understandings' of numbers and the maths that follow them.
What might handicap learning?
When I'm presenting some teacher-training, I often quote from an official and respectable book on US research on how people learn. Part of their second Key Finding (of three) emphasises the importance of using what you know to work out what you don't know. That is what I'm going to try and achieve within this blog. That will require you to indulge me as I explain basic knowledge that you might think you left behind when you were 6 years old. I'm not patronising you. I’m building those foundations without over-reliance on long-term mathematics memory. (You might have a good long-term memory for spelling. Memory is not just one 'memory' for one area of information and facts. It is accepted that there are multiple intelligences. I believe that this implies that there are multiple memories. There is a maths memory. You may not have it.
The power of estimation (approximately)
Returning to that Australian paper of Nothcote and McIntosh. They found that the maths adults do was mainly mental and that almost 60% of all calculations required only an estimate. I could make an argument that some of the maths 'stuff' that adults do, doesn't involve numbers or equations at all. For example, when I cross the street to get to my local grocer, I look at the cars heading towards me and make a judgement as to whether I can cross safely. So far, I have been right. Crossing the road in Mumba, where one of my ex-students lives, invokes its own strategy, 'The Hand of God' (not the Maradonna example for my generation). As a pedestrian you venture out with your hand raised, palm facing the traffic and trust that they will stop or avoid you. That's not maths, that’s faith in your fellow human-beings. Mumbai traffic is a great leveller for maths.
One of my students from when I worked in the US, introduced me to a great saying; "Close enough for Government work". As a Brit in our current political climate, I can relate to that.
In schools, maths problems are set and pupils answers are marked as 'right' or 'wrong' (tick or cross). Rarely are they marked as 'close'. (This doesn’t apply to assays in English lessons). I don’t think there is anywhere to go, or any chance of reasonable follow up to 'wrong'. Unless you use the phrase 'Bigger or smaller?' that is, do you think that the correct answer is bigger or smaller than your answer? You might even go as far as 'a lot bigger' or 'a lot smaller'.
There is nothing wrong with 'wrong'. It's just not very productive or constructive and can be very demotivating (and over-literal), but it's quick for a busy teacher. 'Wrong' is hard to negotiate. Many adults have many years of experiencing this blunt evaluation, so their demotivation may be deeply embedded. Consequently, I have to think of ways in this Blog to overcome that block and encourage you to have another go. I'm asking you to indulge me. It's a big ask, but I hope it results in a positive outcome, which, hopefully, will be to lose that fear of maths and gain some useful skills.
Most of the calculations that adults attempt are mental (which requires good working memory …. More later) and almost 60% of all calculations required only an estimate (which leaves 40% that need an exact answer, Thus more than 50% are about estimation, about being 'close enough.'
I did some research many years ago about how people think when they are 'doing' maths things. What my colleagues and I observed is that some adults (and children) are comfortable with the principle of estimating and some are not. I think that has a lot to do with the belief that answers in maths need to be exactly right and need to be calculated using a formula taught in maths classes. Let me offer a couple of examples where this is unrealistic for the maths of life.
Some thoughts and experiences of estimation:
A meal has cost $128.94 and you want to give a 10% tip to the waiter. (you have estimated that 10% is appropriate) The calculation will involve dividing by 10. Can you do it? The answer will be $12.89. Is that what you will tip?
Or will you round the $12.89 to $13.00? I think a tip of exactly $12.89 seems a little 'picky' or even slightly disapproving (and pedantic). The rounded-up tip of $13.00 seems more generous, even though it is only11c more. Estimation can have an emotional component. And $13.00 is easier to add on to $128.94 than $12.89.
When I used to take my younger daughter shopping, I'd say, 'How long will you be in this shop?' Often she would answer '15 minutes.' Experience had taught me that 15 minutes was very much an under-estimate. When shopping, we had very different perceptions and estimations of time.
Professor Brian Butterworth is a leading expert and pioneer in the study and understanding of dyscalculia. He has been involved in studies on dyscalculia around the world and has written many erudite books (including, 'Fish Can Count' and 'The Mathematical Brain.')
He tells the story that in Australia pupils were taught at school that Aboriginal people only counted 'one, two, three, four and many'.
My story around this is based on a conversation I had with my Aboriginal guides when visiting Uluru (or Ayers Rock) in Australia. I was amused that one guide was called 'Kelly' and other was 'Ned'. I, very sensitively, I hope, asked how they communicated how far they were planning to travel when they set off to visit another settlement. With a big smile, my guide said, 'A little bit long way.' A magical estimate! Which firmly fixed the concept of estimation in my brain. My lovely daughter's shopping equivalent was, 'A little bit very expensive.'
There can be more sophisticated and impactful consequences of dyscalculia. This is from the internet and the Dyscalculia Headlines website on 7/6/2023:
'So my disabilities and I (dyslexia and dyscalculia) made grave mistakes while picking a health insurance plan and now I'll be paying an exorbitant premium every month, plus everything and be out of pocket for this entire year. I'm trying to pay for all of it. Not enough swear words.'
Start at the very beginning (As we learned in 'The Sound of Music'. It’s a very good place to start).
The Rose report on dyslexia (UK) suggested that teaching phonics would be a good intervention for reading problems. It has proven to be successful with reading performance scores around England improving significantly. There is a maths equivalent which my friend and colleague, Mahesh Sharma and I agree upon, that is, the ability to decompose and recompose numbers. For example, to add 7 and 8, you can decompose the 7 and the 8:
7 = 5 + 2 and 8 = 5 + 3 So, 7 + 8 = 5 + 2 + 5 + 3 = 5 + 5 + 2 + 3 = 10 + 2 + 3 = 15
Or 8 + 7 = 8 + 2 + 5 = 10 + 5 = 15
And to multiply 7 x 6 (7 lots of 6). We can use 7 lots as 5 lots of 6, plus 2 lots of 6:
So, 7 x 6 = 5 x 6 plus 2 x 6 = 30 + 12 = 42
Both these examples are using the key numbers 2, 5 and 10 and a basic understanding of addition and multiplication (using partial products).

In lectures and webinars I use visual images to support communication, such as in Figure 1.for 7 x 6.and Figure 2 for number combinations that add to make 10. If you wanted to create a sensory experience for those number bonds, you could use the pieces from a set of draughts.
Linking addition, subtraction, multiplication and division can be like creating mutual support for understanding the four key operations. For example, subtraction is the opposite of addition. Back in those days when we used coins and notes when we were shopping, the shop assistant would sometimes count on to make your change. For example, if you gave them a £5 note for a purchase of £1.83, they might count on to the £1.83 using these steps, putting the relevant coins in your hand as they counted:
'£1.83 plus 2p is £1.85'
'£1.85 plus 5p is £1.90' (Can you see where this is going?)
'£1.90 plus 10p is £2.00'
'£2.00 plus £3.00 is £5.00'
If you add up all the amounts they gave to get to £5, you have £3.17p, the correct change. They may not even articulate that total amount. The counting out was enough. This was, not surprisingly, called 'shopkeeper maths'. It was an everyday way of making maths accessible. Now we often use a credit card to ‘touch and pay’ and so we have no experience of the process of adding on to make change. There is no involvement with the numbers. It would be useful and sensible to estimate, so that rounding up of £1.83 to £2 and subtracting £2 from £5 giving and estimate of 'more than £3 change, but less than £4 change'. The counting on strategy uses those number combinations for 10 from Figure 2.

The example I gave above for working out 7 x 6 links multiplication to addition>
As I said, there is a comparison here with reading:
Fluent reading and fluency in numberness are analogous. Research (Williams, 1995) in reading shows that phonemic awareness - the insight that words are composed of sounds and the ability to connect fluently grapheme to phoneme and phonological sensitivity - the ability to break words into meaningful “chunks” and then “blend” them fluently - are predictors of early reading performance ….(better than IQ tests, readiness scores, or socioeconomic level) and essential for reading acquisition.
We can 'chunk' in number work too.
Let me give you another example of chunking when multiplying. When I was a child, many years ago, we did not have decimal currency, that is coinage based on ten, like our everyday number system, Coinage was based on 12 and on 20. (We changed in to decimal coinage in 1971). The pre-decimal era gave a reason to teach the 12x table of facts (and the fact that there were 12 inches in 1 foot). I loved the word for the number 144, which was the amount you got when multiplying 12 by 12. The word was ‘gross’. These days, it is often used as a slang word with no connection to 144 or 12 x 12. (Figure 3).
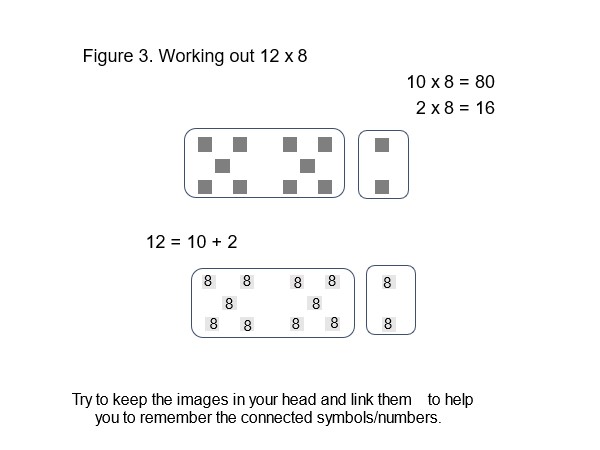
Learning maths is developmental. I'll give you an example now. It extends the idea of breaking down a 'complicated' multiplication into manageable chunks (the maths term is 'partial products', that is parts of the final product.) That is what Williams (above) found.
Numbers, digits and place value
'Chunking' is one very important principle in maths. Let me now try to explain another.
We use ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to represent any number. It's how we combine these symbols that matters. When I lecture about this I often use the image of the 'sheep counters' (Figure 3). It has some good points to make, one of which is that our number system is based on ten and thus 'ten lots of ten' (hundred or century) and ten lots of 'ten lots of ten' (thousand) and so on. There is a pattern, a sequence, that is logical (I will try to convince you that it is logical).
Imagine that there is a sheep farmer with three sons, called One, Ten and Hundred and that they accompany him everyday when he goes to count his sheep.
He shouts out 'Sheep' and the 'one' son puts up one finger for every shout. After 10 shouts the son has used all his fingers, so he nudges the 'Ten' son who puts up one finger. This shout and nudge process goes on until the 'Ten' son has used all of his ten fingers. He nudges the 'Hundred son, who shows one finger, representing one hundred. The finger only represents 1 hundred if the sons keep their places, the order in which they stand. So, in Figure 4 where there are three sheep counters, they are showing exactly 100 sheep: The hundred counter is showing 1 finger and the Tens and Ones counters are showing zero (0) fingers, hence 1 0 0.
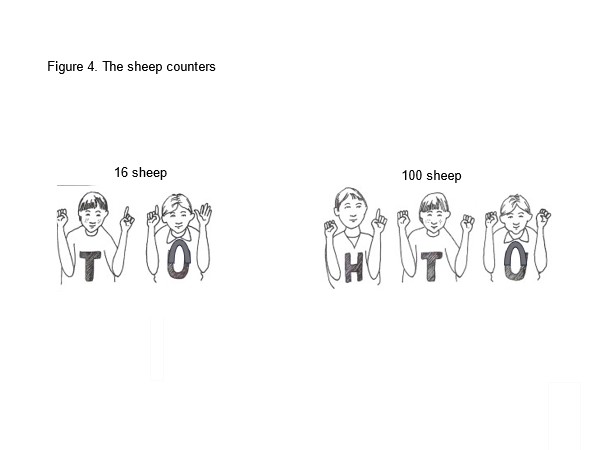
The nudge deals with the change from ones to tens and from tens to ones, Where the digit comes in a number tells us what it represents in ones and tens, so in the number 163, there is 1 (Hundred), 6 (Tens) and 3 (Ones). The place the digit hold in the number tells you its value.
Try these:
827 ___ hundreds ____ tens ____ones
104 ___ hundreds ____ tens ____ones
555 ___ hundreds ____ tens ____ones
Did you get?
827 8 hundreds 2 tens 7 ones
104 1 hundreds 0 tens 4 ones
543 5 hundreds 4 tens 3 ones
The place a digit holds in a number tells you its value. Hence the term 'place value of digits' in numbers. It’s a system that works for all numbers, no matter how big.
Big numbers have their digits grouped
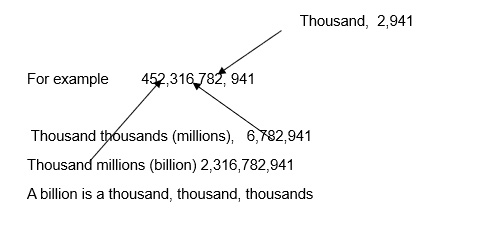
Writing the numbers separately:
2,941 is 2 thousand, 9 hundred, 4 tens and 1 one:
6,782,941 is 6 thousand, 7 hundred, 8 tens (thousands) and 2 thousands, 9 hundred and four tens and 1 one or:
6 million, 7 hundred thousands, 8 ten thousands, 2 one thousands, 9 hundreds and four tens and 1 one.
In the number 452,316,782, 941, the 2 between the 5 and the 3 represents 2 billions
And the 2 between the 8 and the 9 represents 2 thousands
So the PLACE a digit holds in a number can have a massive effect on the VALUE it represents.
Money confusions and place value
Shops often use (close) relationships such as:
They offer a computer for £999 because that looks significantly cheaper than £1000. (it’s a 3-digit number instead of a 4-digit number, but the difference between the two prices is only £1.)
Items may be priced at £19.99 instead of £20 because many shoppers focus on the £19 as being less than £20 (as it is), but the difference in price is only 1 penny.
And whenever I drive anywhere, I am mildly irritated to see petrol (and diesel) prices such as 143.9 or 132.9p per litre. There is no coin that enables me to receive change of 0.1p if I pay 144p for exactly 1 litre.
People can use maths to deceive and/or mislead.
Memories and maths
The Australian research found that much of the maths that adults meet is mental arithmetic. This area of maths demands a good working memory. This is an inherent skill and, varies from person to person. It seems that it cannot be directly trained, though practice will help performance of mental maths, as will secure access to basic facts and maths procedures. Working memory does what its name suggests it does. It’s the memory you use when you are working something out, such as holding one stage in memory as you move to the next stage of a calculation. If you have a poor working memory it is likely that you will lose your place in mid-calculation. Obviously, if you have access to a notepad, that will help.
Sort term memory is a memory again that does what you would expect from its name. It remembers information for a short term. My own biggest problem with short trem memory is remembering the names of people I have just been introduced to. If you can’t remember the maths question that you are trying to solve, it is obvious that you are very unlikely to solve it.
Tests for short term and working memories often involve repeating random sequences of numbers, in the order given for short term memory and reversed for working memory. For example, practicalpie.com. This is a free memory test (5 Mins) – short term, long term, and working memoriesjust .
There is research that has found that working memory capacity is reduced by anxiety.
Things that give me some concern include entries on Pinterest about tricks to do maths. Tricks are less likely to improve comprehension and understandings of maths and often focus on one isolated skill or fact. So, no integration into a compendium of knowledge, but a trick might deal with that isolated issue. I hope I have made the example below clear enough to follow. It’s just for multiplying by 11.
The two-step trick:
12 x 11 separate the 1 and 2 1 2
Then, the second step:
Add the 1 and 2 (=3) and insert the 3 in the middle 132
34 x 11 separate the 3 and 4 3 4
Then, the second step:
Add the 3 and 4 (=7) and insert 7 in the middle 374
45 x 11 separate the 4 and 5 4 5
Then, the second step:
Add the 4 and 5 and insert 9 (4 + 5 = 9) in the middle 495
Or the traditional method 45 x 10 plus 45 x 1 450 + 45 = 495
This method works for any 2-digit multiplication.
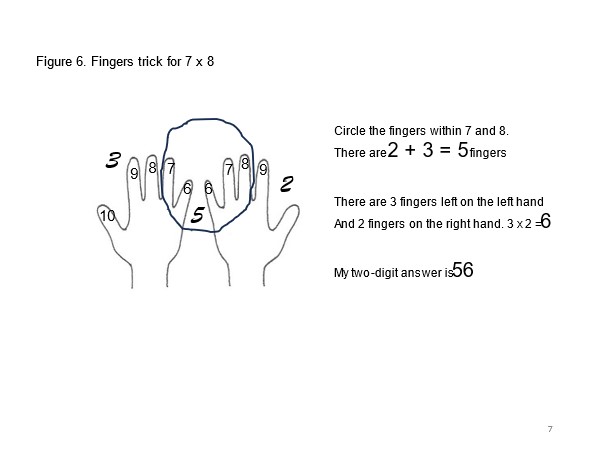
There are several such tricks presented quite often on Pinterest, building to quite a load on long term memory. I think they come across as slick 'one-offs' which are unlikely to improve a general understanding of maths. There are also some gimmicks for 'learning basic facts. These also tend to be one-offs with no comprehension benefits, though the procedure (trick) shown in Figure 6 works for any fact from 6 x 6 to 9 x 9. If you felt motivated you could try it out. Many of these tricks have no visual images to help comprehension. They tend to be symbol-based.
Bear with me while I try to explain a conceptual method for working out 9x facts. I'm using this as a last attempt to convince you that in maths each lesson should be about 'what else are you learning?' Tricks are the opposite of this. They address one facet of the necessary learning. I want the learning to impart a cumulative understanding of maths, using ideas in different situations. That’s developing thinking skills and intelligence. It’s a shame to miss out on that.
So, I’ll break down this next example to show what else is being learned. It's for 9 x 8. Language flexibility: which is best for this example? '9 times 8' '8 multiplied by 9' '9 lots of 8'. The first two interpretations use maths vocabulary, which can be abstract. The last uses general vocabulary and can be readily visualised.
9 times 8 could be visualised as a rectangle, as an area with one side of 9 and the other one as 8 . This is not too useful for this basic calculation
But the form '9 lots of 8' takes us to products, relating the multiplication to repeated addition.
8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8
And then to estimation, where 9 lots of 8 is close to 10 lots of 8 (and is smaller than)
Using key facts: 10 x facts are key (and reminds the learner of place value) 10 x 8 = 80
9 lots of 8 are 1 less 8 than 10 lots of 8, so we subtract one 8 to get to the answer we want
9 x 8 = 80 – 8 = 72

That was a 'bigger or smaller?' a 'more or less?' appraisal of this interim answer.
And it used two partial products, a 10 x 8 and a 1 x 8
Checking and generalising: This works for any answer to a 9x calculation using whole numbers: Add the digits and they will add to make 9 9 x 8 = 7 2 7 + 2 = 9
There is a lot of WEAYT (What Else Are You Teaching) in this example of basic maths. It's about building concepts and understandings.
At last! Last words: It is hard to write about maths difficulties without writing about some actual maths. I hope my choices have given you some confidence.
I know I went on a bit about the background behind maths difficulties, but understanding problems can help us to overcome them. Do try.
Practise estimating answers and check how close you can get. (And check 'bigger' or 'smaller')
If you want more of my visual maths, check out my ‘MathsExplained video tutorials. They are not expensive. What I like about a video is that you don’t have to watch all of it in one go (though it is often worth first taking a big picture overview of all the content.) Then you can watch any bit/section as many times a you wish. Videos don’t lose patience with you. You can shut up my voice and just watch the visual images. You have control. Make notes and be an active learner.
Good luck. Learn to be good enough to feel more confident with maths. Don’t be afraid of being wrong. I find that, because I’m considered to be a maths expert, peoples’ expectations of accuracy from me are very high. No pressure. No shame when I’m wrong. (I end with a lie. That’s not a great principle.)
Thanks for reading this. Steve Chinn













